Theory

Hyperplane Separation Theorem

For 2D

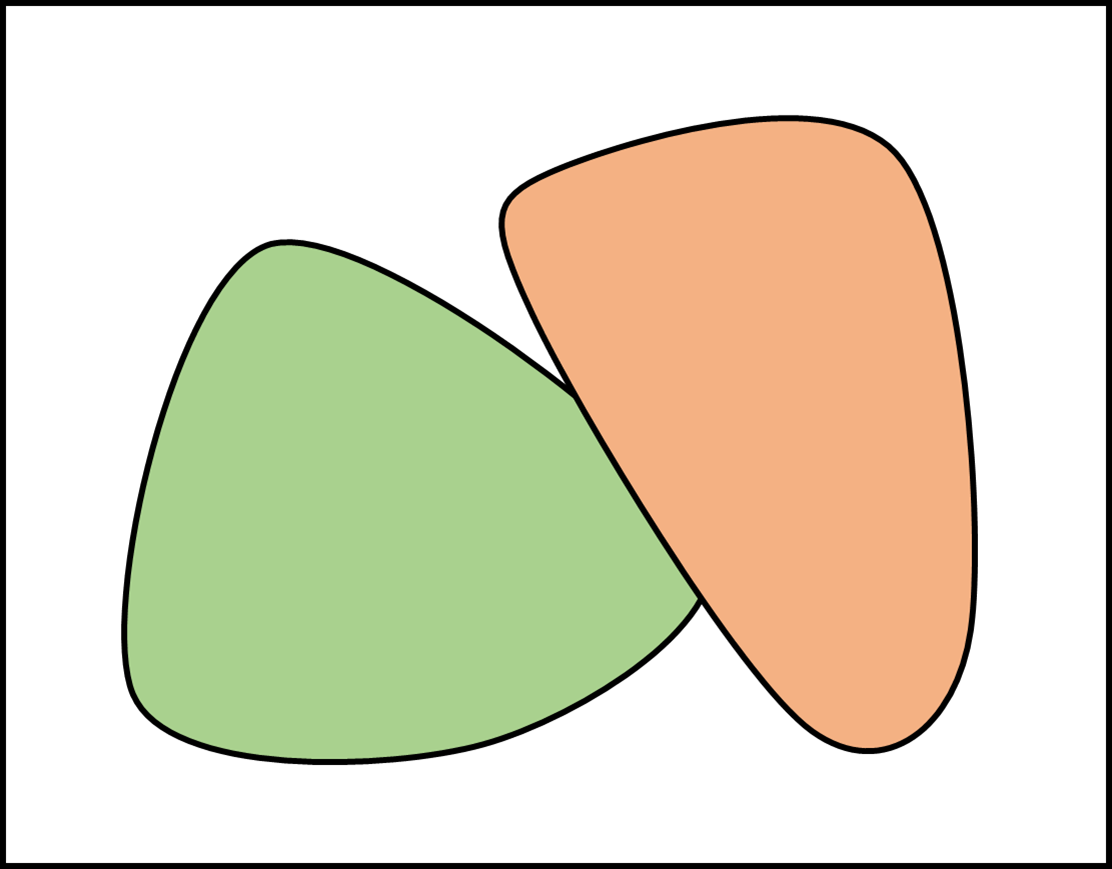
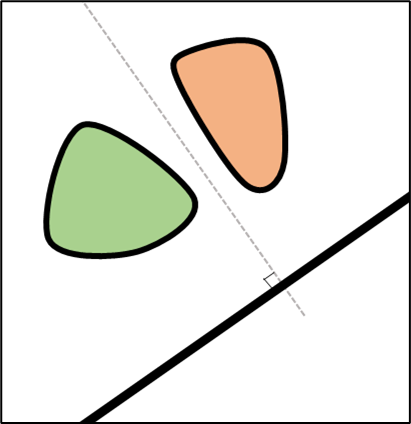
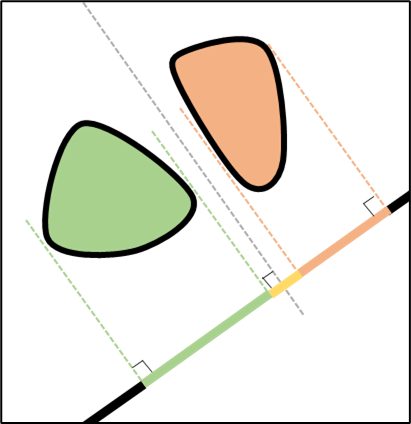
Theorem: If two convex shapes do not collide, then, a straight line can separate them.

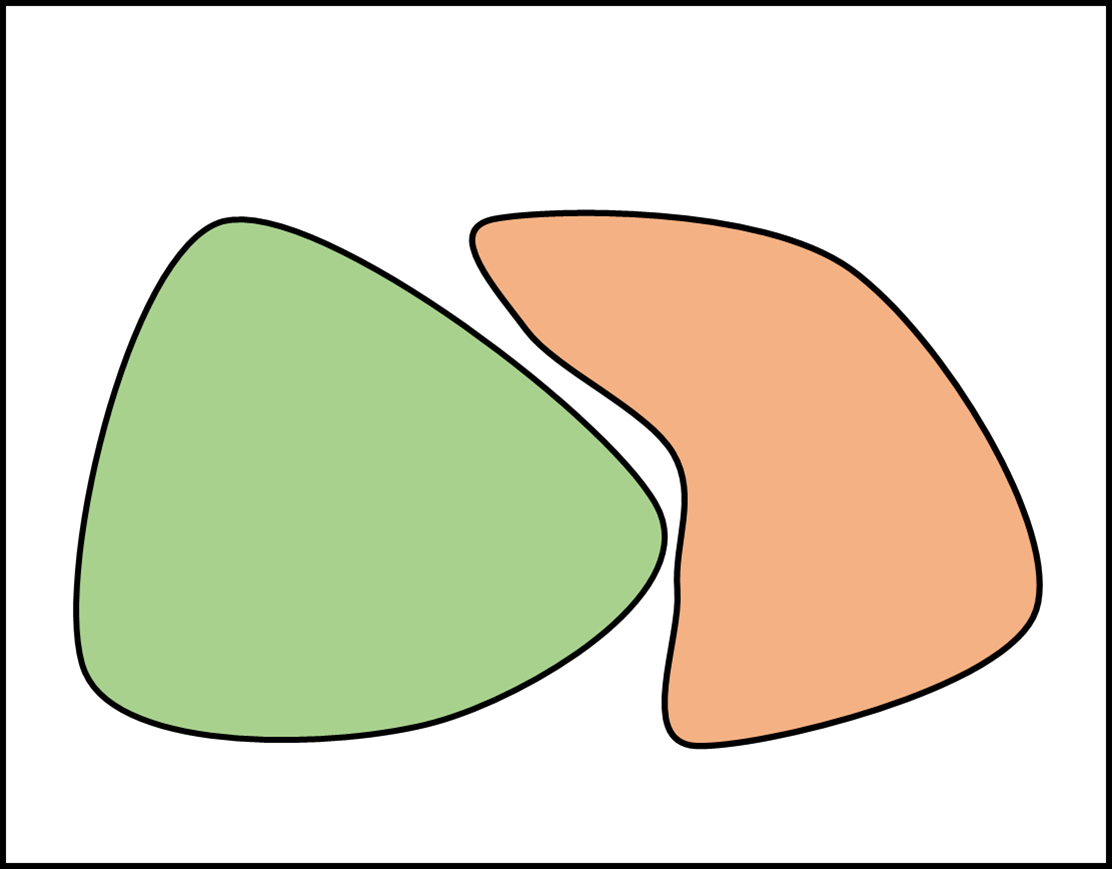
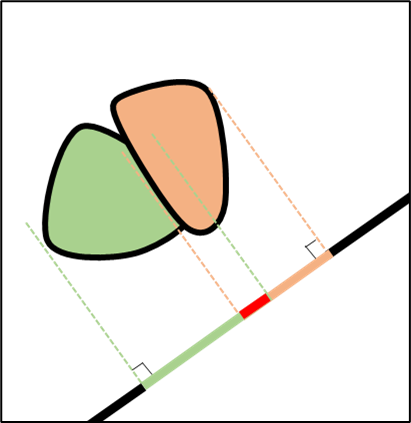
Contrapositive: If two convex shapes collide, then, there is no straight line separating them.

For 3D

Theorem: If two convex shapes do not collide, then, a plane can separate them.

Contrapositive: If two convex shapes collide, then, there is no plane separating them.

Generalization for higher dimensions

Theorem: If two convex shapes do not collide, then, a hyperplane can separate them.

Contrapositive: If two convex shapes collide, then, there is no hyperplane separating them.

Examples :

Separating Axis Theorem

Definition :

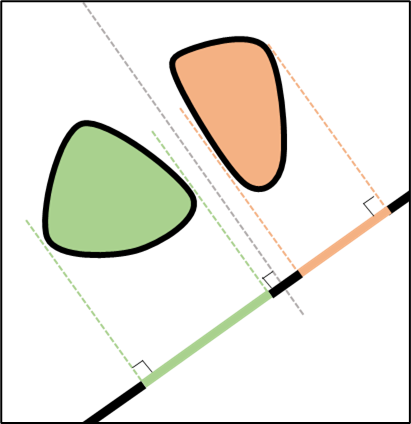
Statement: The line, plane, or hyperplane described above always has a normal axis.

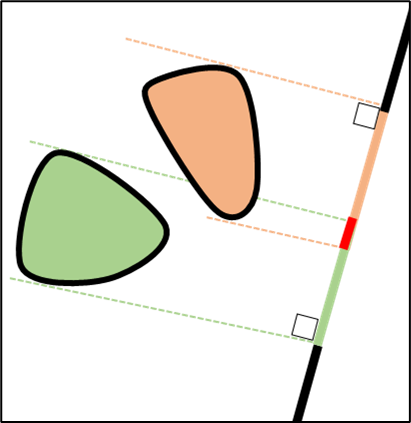
Theorem: If the shapes are not colliding, the projections of the shapes on this axis do not overlap.

Contrapositive: If the shapes are colliding, then, no matter the axis we take, the projections of the shapes on this axis will overlap

Examples :