Projecting Shapes
Projecting a point
The dot product can be used to project a point on an axis.
def ProjectPointOnAxis(point, axis) -> float:
return DotProduct(point, axis);
2D Dot Product
def DotProduct(v1, v2) -> float:
return v1.x * v2.x + v1.y * v2.y
3D Dot Product
def DotProduct(v1, v2) -> float:
return v1.x * v2.x + v1.y * v2.y + v1.z * v2.z
Dot Product Generalization
def DotProduct(v1, v2) -> float:
nbDimensions = v1.GetDimension()
total = 0
for i in range(nbDimensions):
total += v1.coords[i] * v2.coords[i]
return total
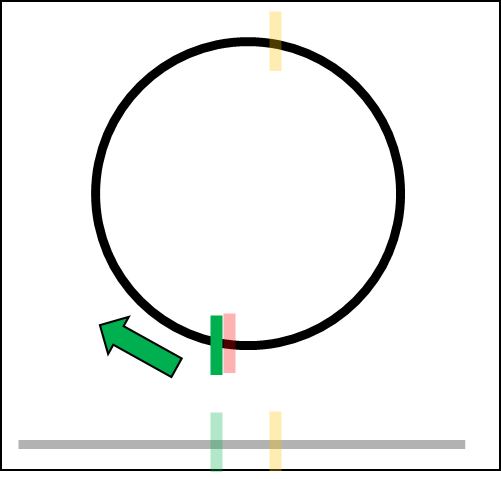
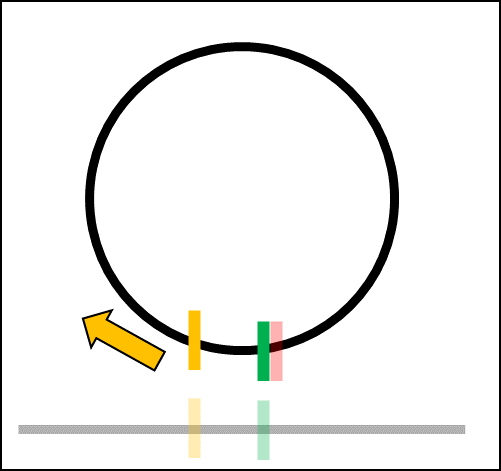
Projecting a circle, sphere, or hypersphere
To simulate an hypersphere, we usually make models with a lot of triangles and vertices.
This is one of the best ways we know to render hyperspheres with other objects.
However, for collisions, we do not need this representation, since it only makes the performance worse.
Instead, we can just use the mathematical properties of the hypersphere and have O(1) performance.
def ProjectSphereOnAxis(hyperSphere: HyperSphere, axis: Vector) -> Range:
centerProj = ProjectPointOnAxis(hyperSphere.center, axis.normalized())
range = new Range()
range.min = centerProj - hyperSphere.radius
range.max = centerProj + hyperSphere.radius
return range
Projecting a polygon
Mostly used shapes are models composed of vertices.
The projection of all the points of an edge is equal to the range of the projection of its two vertices.
def ProjectShapeOnAxis(shape: Shape, axis: Vector) -> Range:
range = new Range()
range.min = Math.max()
range.max = Math.min()
for vertex in shape.vertices:
proj = ProjectPointOnAxis(vertex, axis)
if (proj < range.min):
range.min = proj
if (proj > range.max):
range.max = proj
return range
Projecting a 2D convex polygon
The extremum properties
Definitions
Let S(t) be the parametric equation of a convex shape.\ It returns a point of the shape for a given t.
Let P(t) = DotProduct(S(t), axis).
P(t) is the projection of the points of that shape on a given axis.
Example :
S(t) = r * cos(t) * i + r * sin(t) * j
S(t) represents a circle with a radius of r, centered around the origin.
Properties of S(t)
S(t) represents a closed set, so S(t) is continuous.
S(t) represents a closed set, so S(t) is periodic.
i.e. : if we choose a point and follow the line, we end up looping and coming back to that first point.
Properties of P(t)
P(t) = DotProduct(S(t), axis).
S(t) is continuous. DotProduct is a continuous map.
So P(t) is continuous.
P(t) = DotProduct(S(t), axis).
S(t) is periodic, and axis is constant.
So P(t) is periodic too, with the same period as S(t).
Every local maximum of P(t) is equal to the maximum of P(t).
Every local minimum of P(t) is equal to the minimum of P(t).
Dichotomy
As we saw before, once we find the extremum, we do not have to test the other vertices anymore.
The projections are also continuous, and there are only 2 extremums, so:
# Algorithm created by myself, and proud of it, hehe
def NextIndex(shape, index):
size = len(shape.vertices)
return (index + 1) % size
def PrevIndex(shape, index):
size = len(shape.vertices)
return (index - 1 + size) % size
def GetMiddleIndex(shape, id1, id2):
if (id1 < id2):
return (id1 + id2) / 2
else:
size = len(shape.vertices)
dist = size - (id1 - id2)
return (id1 + dist / 2) % size
def IsSmallerClockwise(shape, axis, index):
p = ProjectPointOnAxis(shape.vertices[index], axis)
pNext = ProjectPointOnAxis(shape.vertices[NextIndex(shape, index)], axis)
return pNext < p
def IsSmallerAntiClockwise(shape, axis, index):
p = ProjectPointOnAxis(shape.vertices[index], axis)
pPrev = ProjectPointOnAxis(shape.vertices[PrevIndex(shape, index)], axis)
return pPrev < p
# This function is tail recursive, so the compiler can optimize it out
def SearchMinProjectionOnAxis(shape: Shape, axis: Vector, minIndex, maxIndex) -> float:
interval = maxIndex - minIndex
i1 = minIndex
i2 = GetMiddleIndex(shape, minIndex, maxIndex) # half
v1 = shape.vertices[i1]
v2 = shape.vertices[i2]
p1 = ProjectPointOnAxis(v1, axis)
p2 = ProjectPointOnAxis(v2, axis)
if (p1 < p2):
# Go in the direction of p1
if (IsSmallerClockwise(shape, axis, i1)):
return SearchMinProjectionOnAxis(shape, axis, i1, i2) # clockwise
if (IsSmallerAntiClockwise(shape, axis, i1)):
return SearchMinProjectionOnAxis(shape, axis, i2, i1) # anti clockwise
# else, already at the end
return p1
elif (p2 < p1):
# Go in the direction of p2
if (IsSmallerClockwise(shape, axis, i2)):
return SearchMinProjectionOnAxis(shape, axis, i2, i1) # clockwise
if (IsSmallerAntiClockwise(shape, axis, i2, i1)):
return SearchMinProjectionOnAxis(shape, axis, i1, i2) # anti clockwise
# else, already at the end
return p2
# The same algorithm can be used to find the maximum projection.
# Cases where projections are equal are not checked, but have to be and can be.
# This program is not optimized, but has for goal to describe how the algorithm works.
def ProjectShapeOnAxis(shape: Shape, axis: Vector) -> Range:
range = new Range()
range.min = SearchMinProjectionOnAxis(shape, axis, 0, len(shape.vertices))
range.max = SearchMaxProjectionOnAxis(shape, axis, 0, len(shape.vertices))
return range
This algorithm is very optimized for a high number of vertices. However, in practice, there are only a few games that have that many vertices in 2D. Due to the different checks, this algorithm is sure to be less optimized for a few amount of vertices.
Examples :
Projecting an arbitrary 2D shape
The brute force way
An arbitrary shape can be constructed with the function S(t), described above.
The brute force way of projecting the shape is just to project every point returned by that function.
Of course, it is impossible to project every point.
That is why we set a precision.
This method does not return the exact projection of the shape, but it is the best we can do without any more precisions on the shape. The performance is also horrible for what it is.
# shape.s(t) returns the vertices of shape
# shape.s(t) is periodic with a period of 1
def ProjectShapeOnAxis(shape: Shape, axis: Vector, precision: int) -> Range:
range = new Range()
range.min = Math.max()
range.max = Math.min()
step = 1 / precision
for i in range(precision))
proj = ProjectPointOnAxis(shape.s(i*step), axis)
if (proj < range.min):
range.min = proj
if (proj > range.max):
range.max = proj
return range
The smarter way
Being a convex shape, the same algorithm applied in the Dichotomy section can be used.
vertices[i] will be replaced by S(t).
Instead of adding 1 to the index, we will add a very small value to t.
Same for removing it.
We could also compute the derivative of P(t) to determine the direction, if possible.
Also, a maximum depth will be used instead of a precision to prevent infinite recursion.
This method does not return the exact projection of the shape either. However, the precision can be very accurate because of the depth we can easily increase thanks to the O(log(n)) complexity of the algorithm.